Survivable Neural Networks
This is a sketch of an idea, and is rather technical. I was inspired by two recent experiences: digging up my graduate research while writing Part II of my three-part series on failure, and reading an incredibly informative article written by Stephen Wolfram on how the popular chatbot ChatGPT works. My research career was focused on defining new problems and solutions for finding a collection of “survivable” routes through a computer network that could survive the failure of any arbitrary components of that network. The underlying structure behind ChatGPT that “learns” how to associate words together to create responses to user text prompts is an artificial neural network. While these are by no means the same type of network, they can be represented by the same abstraction: a graph, or a collection of vertices (aka nodes) connected together by a separate collection of edges (aka links).
In a computer network model, each vertex/node is a device (computer, router, switch, etc.) that is connected to other nodes via edges/links that transmit data between nodes. When represented as a graph, the edges may have weight values, which can represent some cost for using that link (length, dollars, emissions, etc.) that can be fed into something like a shortest path algorithm to find a route for data through the network at minimum cost. Compare this to a neural network model, where each vertex (neuron) represents one of a variety of mathematical functions, and each edge (synapse) similarly has a weight value that changes over time as training examples are fed through the network. As data are fed into the system, each node will perform its mathematical function on the input and send the output to the connected nodes in the next layer of the network, with the weight value on each individual link a factor that transforms the result that arrives at the receiving node. I won’t go into too much more detail on the specifics of how all that works here, since it’s not essential to the idea I’m going to propose - I really do suggest reading Wolfram’s article if you’d like to know more about how neural networks function.
The important bit is that both types of networks can be represented with graphs, and my research work was focused on developing algorithms that can be run on any arbitrary graph, not just ones that represent a computer network. Putting the two together, you could theoretically run my algorithms on a representation of a neural network and get a set of survivable network routes in return that connects the input layer of nodes to the final output layer of nodes in such a way that data can still flow even after a specified set of nodes and links are removed from the network.
More formally, we can take a simplified version of the problem as defined in my final journal paper, which added content-centric network caching to the fundamental problem of connecting a set of data sources to a set of data destinations so that the data can still be transmitted after the removal of some number of network elements in a specified failure set. The caching bit is likely not too relevant, so stripping the problem down to its core essentials, you have the following parameters:
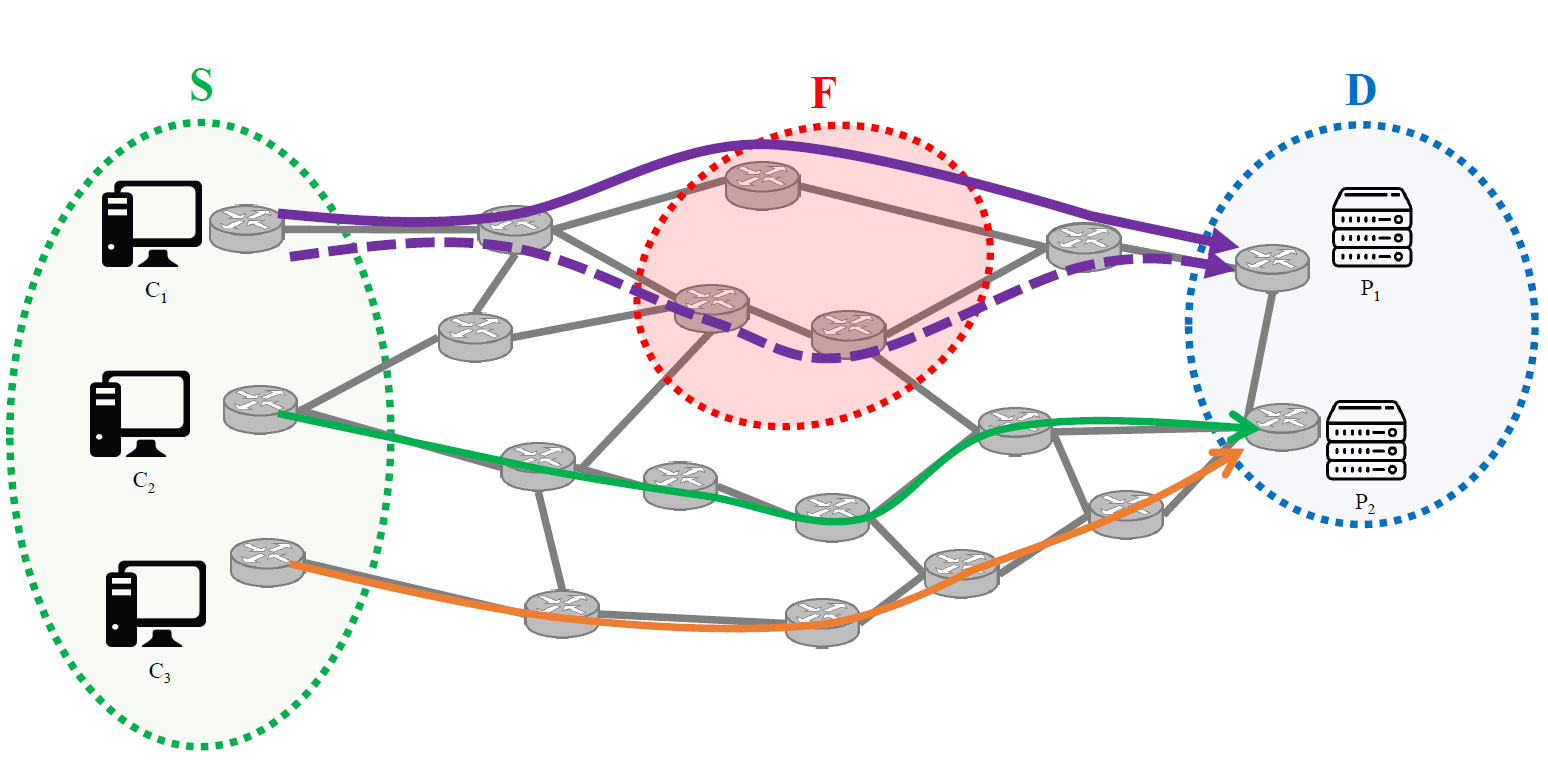
- G = (V,E): The network topology graph, with a set of vertices/nodes V and a set of edges/links E interconnecting those nodes. Each edge in E has a weight value, with the value adjustable for different types of networks and problems - it does not necessarily have to use the weights from the source neural network.
- S: The set of source nodes, through which data is fed into the graph G.
- D: The set of destination nodes, which receive data from nodes in S. A route may go through one or more destination nodes, and every destination does not necessarily have to be at the end of a route - they just have to be reachable by source nodes.
- F: The set of graph elements (nodes and links) that could potentially fail. Both nodes in S and D may be in the failure set. When we assign routes for a given source node, we do consider the routes to be survivable with regard to that particular source, even if that source itself could fail.
- nfe: An integer representing the number of failure events that will occur. Essentially, it is the number of elements of F that will fail at some point, and as such solutions to this problem protect against the failure of any nfe-sized subset of F.
- MinS: The minimum number of sources that must be connected to destinations. Values less than the size of the source set S indicate that not every source must remain connected to a destination in the output solution.
- MinD: The minimum number of destination nodes in D that must be reachable by nodes in the source set S. As with MinS, if MinD is less than the size of the set D, then not every destination node must be in the solution.
- MinCs: The minimum number of connections that must be left originating from a source s after nfe removals from F. A value of 1 for all source nodes indicates that each source must have at least one intact path left over after failure.
- MinDs: The minimum number of destination nodes that a particular source s must be able to reach after failure occurs. Similar to how MinD can be used, values greater than 1 are useful if particular source nodes must be able to transmit their data to more than one destination.
-
An example solution for my problem applied onto a computer network.
-
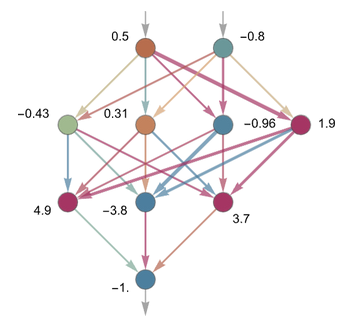
Small neural network topology with weights (sourced from Wolfram's article).
When an algorithm designed to solve the above problem at minimum cost (factoring in the weight of links used) is run on a computer network, you get a “cheap” survivable set of routes for transmitting data from sources to destinations. When you do the same on a neural network graph, you get the same result - a set of routes for transmitting data from source neurons to destination neurons that could survive the removal of a third specified set of neurons and links.
What purpose would such a set of routes serve in a neural network? I’m not certain! It’s possible this wouldn’t be useful at all, but I can certainly speculate. From my readings I’ve seen that a good deal of the state-of-the-art work being done on neural networks is founded in empirical observations rather than underpinned by theory. We find what works through trial-and-error and building on past successes. The composition of the sizable neural networks that make up the core of ChatGPT has been arrived at through experimentation, with entire blocks of “types” of neurons that perform certain mathematical functions chosen for inclusion because they were found to work well.
It’s entirely possible that the current networks we are using, with nodes and links numbering in the millions or billions, are not in the “optimal” form that they could be for solving the problems they are trained to solve. It’s possible that the network could be trimmed down to the “essentials”, whatever exactly they are, and achieve similar performance at a lower cost. Through experimentation with an adapted version of my problem, using algorithms written by professionals that would likely be far more performant than the rather simplistic solutions I created for my dissertation, neural network researchers may be able to work towards discovering the “essential” form of the network that can still solve the desired machine learning problem.
Running such algorithms with a variety of failure sets - ranging from anything in the network for the “most survivable” collection of routes, to specific components of the network like an Attention Block when experimenting with removing different categories of network elements - could help us discover what is needed and what isn’t by running sample data through the trimmed network that is left over after the removal of the failure set and the nodes/links not included in the solution. Increasing the nfe value to make the set of routes resilient to more simultaneous removals would consequently increase the amount of the network that is included, as additional disjoint (non-overlapping) paths would be required to satisfy the survivability requirements, which could help improve the output solution quality due to a greater diversity of available neuron functions. Taking an already trained network and trimming it down could speed up this process, and it would certainly be interesting to see what the resulting output of the network would be!
Conversely, the problem definition could be expanded to include an additional set of nodes if we want these intermediate components to be included in the solution under different requirements than the S or D nodes. I propose the addition of a ‘R’ set of required nodes that data must flow through as the network operates. The elements of the R set can be tuned to the particular neural network being examined - if there are neurons that are found to be essential to the development of coherent output, they can be designated as required for the survivable routes generated for this problem.
Formally, we could add the following parameters:
- R: A set of nodes that data should route through while traversing from nodes in S to nodes in D.
- MinR: The minimum number of nodes in R that must be included in the solution. May range from 1 to the total size of the set R.
- MinRs: The minimum number of nodes in R that a particular source S must route its data through while transmitting to a destination node.
-
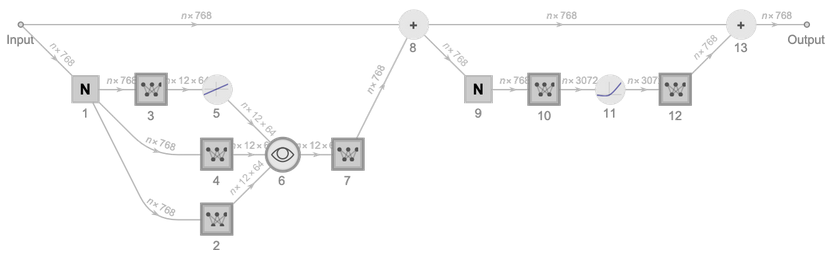
An Attention Block example - some or all of this may be put in the set R to ensure it is used in a solution (sourced from Wolfram's article).
Finally, here are some extra ideas about directions this work could go in:
- Monitor the changes in loss function, which is a measure of how far off a neural network’s solution is to the expected target value, as the network is pruned down to different survivable routes. A decreasing loss could indicate that the pruned network is performing better, or an increase to the loss could show that we are removing the wrong components and negatively impacting performance.
- Calculate a number of different candidate survivable routes, score them on their resilience to failure and ability to solve their intended machine learning problems, and use those high scoring candidates as training data for an entirely separate neural network designed to figure out effective neural network topologies for the intended problem. The solutions generated by that “network-generating network” could be interesting to see be implemented - perhaps there is a pattern not obvious to us yet that determines the effectiveness of the generated networks. Perhaps even new types of neural network layers or blocks could be developed from this process!
- Experiment with different link weights in the neural network model fed into the survivability problem - the weights don’t necessarily have to be the same as the weights used by the original input neural network. Perhaps we could perform analysis on the performance of different input networks, and derive a function that we can apply to the links related to the frequency that different components appear in networks that are successful at performing their intended purpose. If a certain type of neuron, or block of neurons, appears frequently in “good” networks, then we could give the links they use a low weight value, making them more likely to be picked by a minimum-cost (minimum-weight) survivable route solution.
In summation, I think there could be some potential benefit here in determining survivable routes through a neural network - though it may take quite a lot of experimentation to determine what’s “important” in the network, I think pruning a network down to the essentials while maintaining the critical connections from source neurons to destination neurons may reveal new network topologies that could solve problems at lower costs. Or, it may not matter much - perhaps researchers will come up with novel ways of designing their networks to achieve the same goals, or companies will simply throw more money, hardware, and time at the problem.
Either way, I’m excited to be along for the ride as this field advances more rapidly than I think any of us could have expected!